Question

Solve for x.

4x + 12 = 2(2x + 6)
Identify whether the equation has zero, one, or infinitely many solutions.
O zero solutions
one solution
O infinitely many solutions

Answer 1

infinitely many solutions

Explanation:

If we multiply as indicated, 4x + 12 = 2(2x + 6) becomes 4x + 12 = 4x + 12.

This is ALWAYS true, so the given equation has infinitely many solutions.

Answer 2

Infinitely many solutions

Explanation:

`4x + 12 = 2(2x + 6)`

Step 1: distribute on one side of the equation.

`2(2x + 6)\\2\cdot2x = 4x\\2\cdot6=12`

`4x + 12 = 4x + 12`

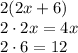
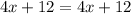
As you can see, this equation is balanced. And we've reached the end of our solution. Although we can still further solve, this result has shown that 4x + 12 is equal to 4x+ 12.

Therefore, this equation has infinitely many solutions.

We could still subtract 12 from both sides.

it would result in zero. So we have:

`4x=4x\\`

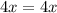
This means 4 divided by 4. Four divide by four is 1

`=1`

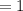
The equation would still have infinite ways of solving it.