Question

Two similar triangles have a pair of

corresponding sides of length 12 meters and 8
meters. The larger triangle has an area of 180
square meters. Find the area of the smaller triangle.

Answer 1

The area of the smaller triangle is 80m²

Explanation:

Find the scale factor to get the dimensions of the smaller triangle from the larger triangle using the given information:

`\frac{\text{Large Triangle Length}}{\text{Small Triangle Length}}=(12)/(8)=(3)/(2)`

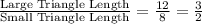
When scaling the area of similar shapes, we will square the scale factor for the lengths. We do this because area is a 2-dimensional measurement.

`((3)/(2))^2=(9)/(4)`

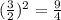
Let x represent the area of the smaller triangle. So, we have:

`(9)/(4)=(180)/(x)`

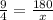
Cross multiply:

`9x=4(180)`

`9x=270`

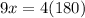
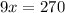
Divide by 9:

`x=(720)/(9)`

`x=80`

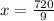
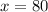
Therefore, the area of the smaller triangle is
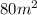`80m^2`.