Question

A rectangular vegetable patch has a perimeter of 28 meters and an area of 48 square

meters. What are the dimensions of the vegetable patch?
meters by
meters

Answer 1

Length = 8 meters

Width = 6 meters

Explanation:

Given the following information:

Perimeter of a rectangular vegetable patch: 2(L + W) = 28 meters

Area = L × W = 48 m²

We can solve for the dimensions by using both equations.

First, let's use the formula for the perimeter of the rectangular vegetable patch, and isolate one of the given variables:

2(L + W) = 28

Divide both sides by 2:

`(2(L + W))/(2) = (28)/(2)`

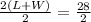
L + W = 14

Subtract W from both sides to isolate L:

L + W - W = 14 - W

L = 14 - W

Next, we'll take the formula for the area, and substitute the value for the L from our previous step:

A = 48 = L × W

48 = W × (14 - W)

Distribute W into the parenthesis:

48 = 14W - W²

Add W² and subtract 14W to both sides:

W² - 14W + 48 = 14W - 14W - W² + W²

W² - 14W + 48 = 0 ⇒ This represents a quadratic equation in standard form. We can use the coefficient and constant values to solve for its roots.

a = 1, b = -14, and c = 48

Substitute these values into the quadratic equation:

`x = \frac{-b +/- \sqrt{b^(2)-4ac}}{2a}`

`x = \frac{14 +/- \sqrt{(-14)^(2)-4(1)(48)}}{2(1)}`

`x = (14 +/- √(196-192))/(2)`

`x = (14 +/- √(4))/(2)`

`x = (14 + 2)/(2)`,
`x = (14 - 2)/(2)`

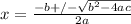
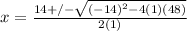
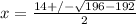
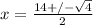
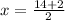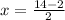
x = 8, x = 6

Now, we can substitute these values into the formulas for the perimeter and area to find the true dimensions of the rectangular vegetable patch.

Perimeter: 2(L + W) = 2(8 + 6) = 28 meters

Area = L × W = 8 × 6 = 48 m²

Therefore, the dimensions of the rectangular vegetable patch are:

Length = 8 meters

Width = 6 meters

Dimensions: 8 × 6 meters.