Answer:
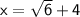

Explanation:
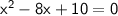
Equations of the form ax^2+bx+c=0 can be solved by the quadratic formula:

Quadratic formula gives you two solutions one when (±) addition and one when (±) is a subtraction:
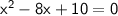
Substitute:
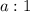
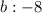
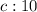
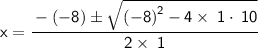
Square -8, and multiply -4 by 10:
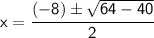
Add 64 and - 40, and take the square root of 24:
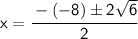
-(-8)= 8
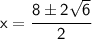
Now solve when (±) is a plus and then solve when it is a minus:-
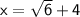

____________________________