Question

Evaluate the integral. (Use C for the constant of integration.) 7x3 5x2 49x 5 (x2 1)(x2 7) dx

Answer 1

`(7)/(2)ln(|x^2+1|)+(5)/(√(7))arctan((x)/(√(7)))+C`

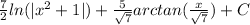
Explanation:

Perform the partial fraction decomposition

`\int{(7x^3+5x^2+49x+5)/((x^2+1)(x^2+7)) } \, dx\\ \\(7x^3+5x^2+49x+5)/((x^2+1)(x^2+7))=(Ax+B)/(x^2+1)+(Cx+D)/(x^2+7)\\ \\7x^3+5x^2+49x+5=(x^2+7)(Ax+B)+(x^2+1)(Cx+D)\\\\7x^3+5x^2+49x+5=Ax^3+Bx^2+7Ax+7B+Cx^3+Dx^2+Cx+D\\\\7x^3+5x^2+49x+5=Ax^3+Cx^3+Bx^2+Dx^2+7Ax+Cx+7B+D\\\\7x^3+5x^2+49x+5=x^3(A+C)+x^2(B+D)+x(7A+C)+7B+D`

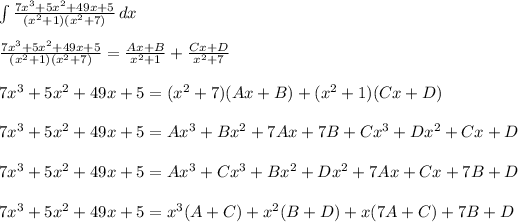
Set up a system of equations and solve for each constant

`\begin{cases} A + C = 7\\B + D = 5\\7 A + C = 49\\7 B + D = 5 \end{cases}`

`A+C=7\\A=7-C`

`7A+C=49\\7(7-C)+C=49\\49-7C+C=49\\49-6C=49\\-6C=0\\C=0`

`A=7-C\\A=7-0\\A=7`

`B+D=5\\B=5-D`

`7B+D=5\\7(5-D)+D=5\\35-7D+D=5\\35-6D=5\\-6D=-30\\D=5`

`B=5-D\\B=5-5\\B=0`

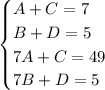
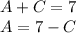
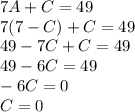
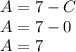
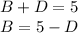
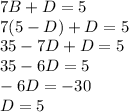
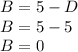
Plug solved constants in and evaluate

`(7x^3+5x^2+49x+5)/((x^2+1)(x^2+7))=(Ax+B)/(x^2+1)+(Cx+D)/(x^2+7)\\\\(7x^3+5x^2+49x+5)/((x^2+1)(x^2+7))=(7x+0)/(x^2+1)+(0x+5)/(x^2+7)\\\\(7x^3+5x^2+49x+5)/((x^2+1)(x^2+7))=(7x)/(x^2+1)+(5)/(x^2+7)`

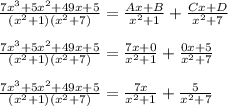
Break up integral

`\int {\bigr((7x)/(x^2+1)+(5)/(x^2+7)\bigr) } \, dx`

`\int {(7x)/(x^2+1) } \, dx +\int {(5)/(x^2+7)} \, dx\\\\\int {(7x)/(x^2+1) } \, dx +5\int {(1)/(x^2+7)} \, dx`

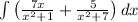
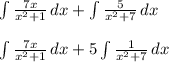
Solve first integral

Let
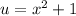`u=x^2+1` and
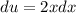`du=2xdx` for the first integral. Thus,
`(7)/(2)du=7xdx`:

`(7)/(2)\int {(du)/(u)}\\\\(7)/(2)ln(|u|)+C\\ \\(7)/(2)ln(|x^2+1|)+C`

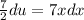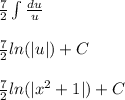
Solve second integral

Since
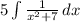`5\int {(1)/(x^2+7) } \, dx` is in the form of
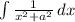`\int{(1)/(x^2+a^2) } \, dx`, its formula is
`(1)/(a)arctan((x)/(a))+C`:

`5\int {(1)/(x^2+7) } \, dx\\\\5\bigr((1)/(√(7))arctan((x)/(√(7)))+C\bigr)\\\\(5)/(√(7))arctan((x)/(√(7)))+C`

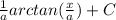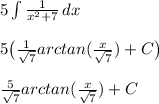
Combine integrals

`\biggr[(7)/(2)ln(|x^2+1|)+C\biggr]+\biggr[(5)/(√(7))arctan((x)/(√(7)))+C\biggr]\\ \\(7)/(2)ln(|x^2+1|)+(5)/(√(7))arctan((x)/(√(7)))+C`