Answer:
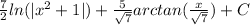
Explanation:
Perform the partial fraction decomposition
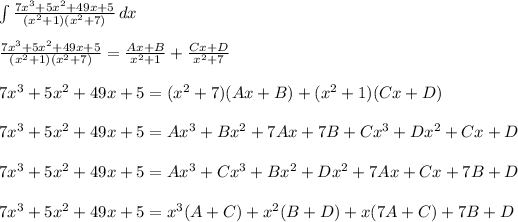
Set up a system of equations and solve for each constant
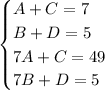
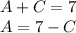
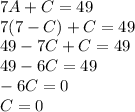
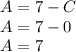
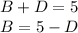

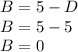
Plug solved constants in and evaluate
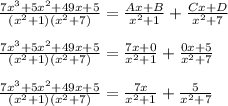
Break up integral
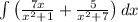
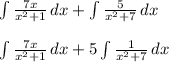
Solve first integral
Let
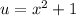 and
and
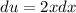 for the first integral. Thus,
for the first integral. Thus,
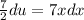 :
:
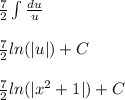
Solve second integral
Since
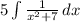 is in the form of
is in the form of
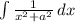 , its formula is
, its formula is
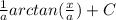 :
:
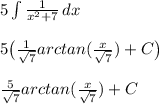
Combine integrals
![\biggr[(7)/(2)ln(|x^2+1|)+C\biggr]+\biggr[(5)/(√(7))arctan((x)/(√(7)))+C\biggr]\\ \\(7)/(2)ln(|x^2+1|)+(5)/(√(7))arctan((x)/(√(7)))+C](https://img.qammunity.org/2023/formulas/mathematics/college/bc61u5v6nz55lkutanfijwqa8s84lzn9v0.png)