Answer:

Explanation:
We are given the function:

Given that p(x) = 832.5, we want to determine two possible values of x.
We can substitute:
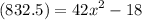
Adding 18 to both sides yields:
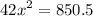
And dividing both sides by 42 yields:
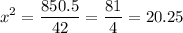
We can take the square root of both sides. Since we are taking an even root, we will need plus/minus. Hence:
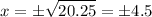
In conclusion, x = 4.5 or x = -4.5.