Answer:
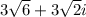 and
and
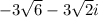
Explanation:
For a complex number
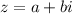 in rectangular form, polar form is
in rectangular form, polar form is
![z=r[cos(\theta)+isin(\theta)]](https://img.qammunity.org/2023/formulas/mathematics/college/3q8e86dqpzjrfepydfvz4r9xnchj7hirpr.png) where
where
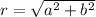 and
and
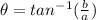 :
:
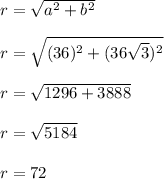
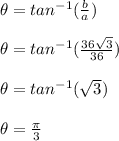
Thus, our complex number in polar form is
![z=72[cos((\pi)/(3))+isin((\pi)/(3))]](https://img.qammunity.org/2023/formulas/mathematics/college/zt11ok6qi8xu1du1uqjti76khzzi1cln8i.png) . This will help us determine the square roots of the complex number using the formula
. This will help us determine the square roots of the complex number using the formula
![\sqrt[n]{r}\biggr[cis\bigr({(\theta+2\pi k)/(n))\biggr]](https://img.qammunity.org/2023/formulas/mathematics/college/gpu4cvcc1mrrx8d7l22we0s2sj1ooe5uhl.png) for
for
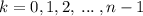 . Note that
. Note that
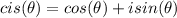 :
:
1st square root for k = 2-1 = 1
![\sqrt[n]{r}\biggr[cis\bigr({(\theta+2\pi k)/(n))\biggr]](https://img.qammunity.org/2023/formulas/mathematics/college/gpu4cvcc1mrrx8d7l22we0s2sj1ooe5uhl.png)
![\sqrt[2]{72}\biggr[cis\bigr({((\pi)/(3)+2\pi(1))/(2))\biggr]](https://img.qammunity.org/2023/formulas/mathematics/college/2palvfjmquw5vyt3scbe4huycrgesf8z0y.png)
![6√(2)\biggr[cis\bigr({((\pi)/(3)+2\pi)/(2))\biggr]](https://img.qammunity.org/2023/formulas/mathematics/college/ogpsqek1njbq1wa3l1kzkcfkt1rfnoc2s9.png)
![6√(2)\biggr[cis\bigr((\pi)/(6)+\pi)\biggr]](https://img.qammunity.org/2023/formulas/mathematics/college/vm9tfkzl8nin6ms31lb58ozf3mcfca59xk.png)
![6√(2)\biggr[cis\bigr((7\pi)/(6))\biggr]](https://img.qammunity.org/2023/formulas/mathematics/college/835ortx4c40ve66fhm4ne85odwjqjubpu3.png)
![6√(2)\biggr[cos((7\pi)/(6))+isin((7\pi)/(6))\biggr]\\ \\6√(2)(-(√(3))/(2)-(1)/(2)i)\\\\-3√(6)-3√(2)i](https://img.qammunity.org/2023/formulas/mathematics/college/7oh8hf4cvd2wuzgvd47dz593mx1dpf5j52.png)
2nd square root for k = 1-1 = 0
![\sqrt[6]{72}\biggr[cis\bigr({((\pi)/(3)+2\pi(0))/(2)\bigr)\biggr]](https://img.qammunity.org/2023/formulas/mathematics/college/ebgvpqkdjuz6hq5t5h0ev5k7p8qm5z4eg8.png)
![6√(2)\biggr[cis((\pi)/(6) )\biggr]](https://img.qammunity.org/2023/formulas/mathematics/college/yjou9nynj7tt0ruk5rrjnd3o8grl8h0fsg.png)
![6√(2)[cos((\pi)/(6))+isin((\pi)/(6))]\\ \\6√(2)((√(3))/(2)+(1)/(2))\\\\3√(6)+3√(2)i](https://img.qammunity.org/2023/formulas/mathematics/college/uk3okykrohhzi9dgr5j3p9zk1ed7847hn2.png)
Therefore, the square roots of
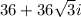 are
are
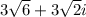 and
and
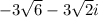 .
.