
We have to prove that:
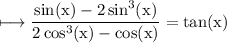
Taking LHS, we get:
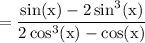
We can take sin(x) as common from numerator part. We get:
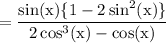
Similarly, we can take cos(x) as common from first two terms. We get:
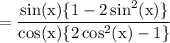
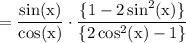
As we know that:
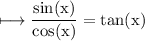
We get:
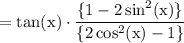
Now, we will expand the terms in fraction:
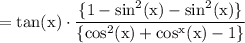
As we know that:
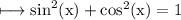
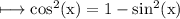
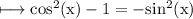
Now substitute the values in the expression, we get:
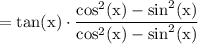
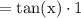
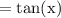
Here, we notice that LHS = RHS
Proved.