Question

What is the recursive formula for this sequence?

10, 14, 18, 22, 26,...
O A. (
= 4
len = 2n-1 +10
=
O B.
ay = 30
an = an-1 + 4
=
C.
(ay = 10
lan= any +4
O D.
ſay = 10
Lan = an-1-4
lan

Answer 1

`\begin{cases}a_1 = 10\\a_(n+1) = a_n + 4\end{cases}`

==================================================

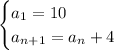
Step-by-step explanation:

The first row
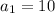`a_1 = 10` indicates the first term is 10. The small "1" is the index number. That means
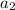`a_2` is next followed by
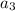`a_3` and so on.

To generate the next term, we follow this recursive step:
`a_(n+1) = a_n + 4`

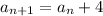
It means "whatever the nth term
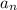`a_n` is, we add 4 to it to get the next term
`a_(n+1)`"

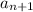In other words, we add 4 to each term to get the next term.

Eg: 10+4 = 14 and 14+4 = 18

The recursive step could be rewritten as
`a_n = a_(n-1)+4` based on how you frame things.