\rm \lim \limits_(n \to \infty ) {n}^{ - (1)/(2) ( (n + 1)/(n) )} (1 * {2}^(2) * {3}^(2) * \dots * {n}^(n) {)}^{ \frac{1}{ {n}^(2) } }​ \rule{200pt}{2pt} \rm I= \sum \limits_(k …

Question

`\rm \lim \limits_(n \to \infty ) {n}^{ - (1)/(2) ( (n + 1)/(n) )} (1 * {2}^(2) * {3}^(2) * \dots * {n}^(n) {)}^{ \frac{1}{ {n}^(2) } }`​


`\rule{200pt}{2pt}`

`\rm I= \sum \limits_(k = 1)^(98) \int_(k)^(k + 1) (k + 1)/(x (x+ 1)) \: dx, then \\`
`\rm[A] \phantom{gg}I>log_e99 \\ \\ \rm [B] \phantom{gg}I < log_e99 \\ \\ \rm[C] \phantom{hffgg} I < (49)/(50) \\ \\ \rm[D] \phantom{gfffg} I > (49)/(50) \\`​

Answer 1

Using the exp-log technique,

`\displaystyle \lim_(n\to\infty) \frac{\left(1 * 2^2 * 3^3 * \cdots * n^n\right)^{\frac1{n^2}}}{n^{(n+1)/(2n)}}`

`\displaystyle = \exp\left(\lim_(n\to\infty) (\ln\left(\prod\limits_(k=1)^n k^k\right))/(n^2) - (n+1)/(2n) \ln(n)\right)\right)`

`\displaystyle = \exp\left(\lim_(n\to\infty) (\sum\limits_(k=1)^n k\ln(k))/(n^2) - (n+1)/(2n) \ln(n)\right)\right)`

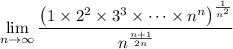
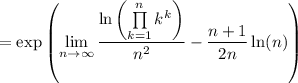
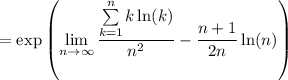
We have ln(k) = ln(k/n) + ln(n), and so we can rewrite the limand as

`\displaystyle = \exp\left(\lim_(n\to\infty) \left(\frac1n \sum\limits_(k=1)^n \frac kn \ln\left(\frac kn\right) + (\ln(n))/(n^2) \sum_(k=1)^n 1 - (n+1)/(2n) \ln(n)\right)\right)`

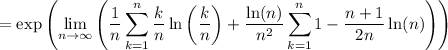
Then the first sum converges to a definite integral,

`\displaystyle \lim_(n\to\infty) \frac1n \sum_(k=1)^n \frac kn \ln\left(\frac kn\right) = \int_0^1 x \ln(x) \, dx = -\frac14`

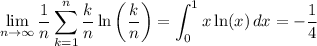
while the remaining terms vanish since

`\displaystyle (\ln(n))/(n^2) \sum_(k=1)^n 1 = (\ln(n))/(n^2) * \frac{n(n+1)}2 = (n+1)/(2n)\ln(n)`

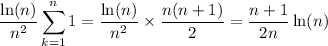
So the limit is
`\boxed{e^(-1/4)}`.

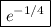Since

`\frac1{x(x+1)} = \frac1x - \frac1{x+1}`

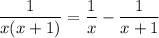
it's easy to show that the integral reduces to

`\displaystyle \int_k^(k+1) (k+1)/(x(x+1)) \, dx = (k+1) \ln\left(((k+1)^2)/(k(k+2))\right)`

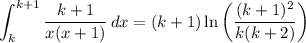
so we can write the sum as

`I = \displaystyle \sum_(k=1)^(98) \int_k^(k+1) (k+1)/(x(x+1)) \, dx = \sum_(k=2)^(99) k \ln\left((k^2)/(k^2-1)\right)`

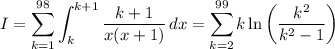
We have k²/(k² - 1) > 1 for all k, so that ln(k²/(k² - 1)) > ln(1) = 0. We can see the first 3 terms of the sum already exceed 1 > 49/50, so (D) is true.

Numerical computation of the sum suggests I < ln(99), but I have yet to come up with an analytical solution for this bound...