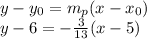Question

Write an equation of a line through (5,6) and perpendicular to the line through (4,8) and (-2,-18)

need this for test

Answer 1

y=-3/13x+7.15384615385

Explanation:

y=mx+b

We want to find the slope first so will find the slope of the line that is perpendicular to our line.

y2-y1/x2-x1

-18-8/-2-4=

-26/-6=

13/3

The slope of the other line is 13/3

To find the slope of our line we can do the opposite reciprocal of 13/3 which is -3/13.

Let's plug that in with the other values to find y-intercept

6=-3/13*5+b

6=-1.15384615385+b

b=7.15384615385

I have no idea why our number is super weird but um yea

Answer 2

`y-6=-\frac3{13}(x-5)`

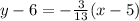
Explanation:

Get the slope of the line between the two points. As usual,
`m= (\Delta y)/(\Delta x)= (8-(-18))/(4-(-2))=(8+18)/(4+2)=(26)/(6)=\frac{13}3`

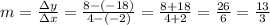
You want the perpendicular to it, so take it's inverse and change its sign:

`m_p=-\frac3{13}`

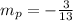
At this point, it's just using the point-slope form, and you're done - unless you're required to provide the line in a specific way, which usually means just crunching numbers and rewriting the equation

`y-y_0=m_p(x-x_0)\\y-6=-\frac3{13}(x-5)`