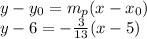Answer:
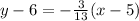
Explanation:
Get the slope of the line between the two points. As usual,
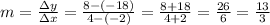
You want the perpendicular to it, so take it's inverse and change its sign:
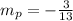
At this point, it's just using the point-slope form, and you're done - unless you're required to provide the line in a specific way, which usually means just crunching numbers and rewriting the equation