Answer:
3y-2=10
Explanation:
Given;
Which of the following does Not belong to the group?
2x > 5 - x
3(x-4)
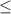 -23
-23
3y - 2 = 10
a < 13a + 1
Solve;
Base on the given data, we can infer that "3y-2=10" does Not belong to the group. You can see that other have Python. Python has six comparison operators: less than ( < ), less than or equal to ( <= ), greater than ( > ), greater than or equal to ( >= ), equal to ( == ), and not equal to ( != ). While, "3y-2=10" doesn't have one.
As well as if you simplify/solve these other will be given as a fraction while "3y-2=10" answer is a whole number.
Solution of each given answer choice;
2x > 5 - x
Add x to both sides
2x + x > 5 - x + x
Simplify
3x > 5
Divide both sides by 3
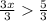
x
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
3 ( x - 4)
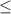 - 23
- 23
![3\left(x-4\right)\le \:-23\quad :\quad \begin{bmatrix}\mathrm{Solution:}\:&\:x\le \:-(11)/(3)\:\\ \:\mathrm{Decimal:}&\:x\le \:-3.66666\dots \\ \:\mathrm{Interval\:Notation:}&\:(-\infty \:,\:-(11)/(3)]\end{bmatrix}](https://img.qammunity.org/2023/formulas/mathematics/college/9ytwodutxmrqcvd4gm8r6d2s5hh08lcq63.png)
Divide both sides by 3
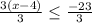
Simplify
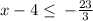
Add 4 to both side
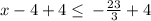
Simplify
x
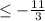
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
3y-2 = 10
Add 2 to both sides
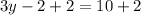
Simplify
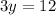
Divide both sides by 3
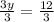
Simplify
y = 4
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
a>13a+1

Subtract 13a from both sides
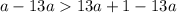
Simplify
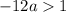
Multiply both sides by -1 (reverse the inequality)
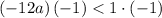
Simplify
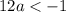
Divide both sides by 12
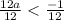
Simplify
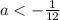
Hence, Now you can infer that "3y-2=10" does not belong to the group.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
~Learn with Lenvy~