Question

Nonsense will be reported!!​

Answer 1

3y-2=10

Explanation:

Given;

Which of the following does Not belong to the group?

2x > 5 - x

3(x-4)
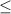`\leq` -23

3y - 2 = 10

a < 13a + 1

Solve;

Base on the given data, we can infer that "3y-2=10" does Not belong to the group. You can see that other have Python. Python has six comparison operators: less than ( < ), less than or equal to ( <= ), greater than ( > ), greater than or equal to ( >= ), equal to ( == ), and not equal to ( != ). While, "3y-2=10" doesn't have one.

As well as if you simplify/solve these other will be given as a fraction while "3y-2=10" answer is a whole number.

Solution of each given answer choice;

2x > 5 - x

Add x to both sides

2x + x > 5 - x + x

Simplify

3x > 5

Divide both sides by 3

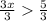
`(3x)/(3) > (5)/(3)`

x
`x=(5)/(3)`

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

3 ( x - 4)
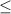`\leq` - 23

`3\left(x-4\right)\le \:-23\quad :\quad \begin{bmatrix}\mathrm{Solution:}\:&\:x\le \:-(11)/(3)\:\\ \:\mathrm{Decimal:}&\:x\le \:-3.66666\dots \\ \:\mathrm{Interval\:Notation:}&\:(-\infty \:,\:-(11)/(3)]\end{bmatrix}`

Divide both sides by 3

`(3\left(x-4\right))/(3)\le (-23)/(3)`

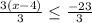
Simplify

`x-4\le \:-(23)/(3)`

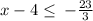
Add 4 to both side

`x-4+4\le \:-(23)/(3)+4`

Simplify

x
`\leq -(11)/(3)`

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

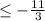
3y-2 = 10

Add 2 to both sides

`3y-2+2=10+2`

Simplify

`3y=12`

Divide both sides by 3

`(3y)/(3)=(12)/(3)`

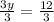
Simplify

y = 4

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

a>13a+1

`a > 13a+1\quad :\quad \begin{bmatrix}\mathrm{Solution:}\:&\:a < -(1)/(12)\:\\ \:\mathrm{Decimal:}&\:a < -0.08333\dots \\ \:\mathrm{Interval\:Notation:}&\:\left(-\infty \:,\:-(1)/(12)\right)\end{bmatrix}`

Subtract 13a from both sides

`a-13a > 13a+1-13a`

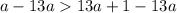
Simplify

`-12a > 1`

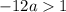
Multiply both sides by -1 (reverse the inequality)

`\left(-12a\right)\left(-1\right) < 1\cdot \left(-1\right)`

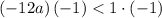
Simplify

`12a < -1`

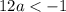
Divide both sides by 12

`(12a)/(12) < (-1)/(12)`

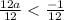
Simplify

`a < -(1)/(12)`

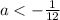
Hence, Now you can infer that "3y-2=10" does not belong to the group.

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

~Learn with Lenvy~