Question

Find all the zeros of the quadratic function y=x²-9x+20

Answer 1

Roots: x = 5; x = 4

Explanation:

Given the quadratic equation, x² -9x + 20 = 0

where a = 1, b = -9, and c = 20

Determine the nature and number of solutions based on the discriminant, b² - 4ac:

b² - 4ac = (-9)² - 4(1)(20) = 1

Since b² - 4ac > 0, then it means that the equation will have two real roots.

Use the Quadratic Formula:

`x = \frac{-b +/- \sqrt{b^(2) - 4ac} }{2a}`

`x = \frac{-(-9) +/- \sqrt{(-9)^(2) - 4(1)(20)} }{2(1)}`

`x = (9 +/- √(1))/(2)`

`x = (9 + 1)/(2); x = (9 - 1)/(2)`

`x = (10)/(2); x = (8)/(2)`

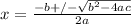
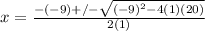
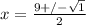
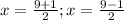
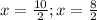
x = 5; x = 4

Therefore, the roots of the quadratic equation are: x = 5; x = 4.