Explanation:
Step 1: Take the First Derivative This means only differentiate once.
Disclaimer: Since absolute value only take positve outputs and quadratics only take positve outputs, we can get rid of the absolute value signs so we now have
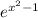
We have the function x^2-1 composed into the function e^x.
So we use chain rule
Which states the derivative of a function composed is the
derivative of the main function times the derivative of the inside function.
So the derivative of the main function is
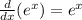
Then we replace x with x^2-1
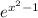
Then we take the derivative of the second function which is 2x so qe multiply them
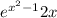
Step 2: Set the equation equal to zero.
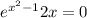
Since e doesn't reach zero. We can just set 2x=0.

So the critical point is 0.
Since e^x will never reach zero
Since 0 is the only critical point, this where the max or min will occur at.
Next we pick any numbergreater than zero, and plug them in the derivative function which gives us a positve number.
Any pick less than zero will give us a negative number.
Since the function is decreasing then increasing, we have a minimum.
Since 0 is the only critical point, we have a absolute minimum at 0.
To find the y coordinate, plug 0 in the orginal function.
Which gives us
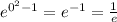
So the minimum occurs at
(0,1/e).