Question

Help pls
tysm in advance

Answer 1

`\bold{\huge{\underline{ Solution }}}`

Given :-

• We have given some information in the above table

To Find :-

• We have to find the mean, median and mode of the given data.

Let's Begin :-

For completion of table you should know the basics formulas :-

• For calculating x( mid point)

`\sf{=}{\sf{(Sum \:of\: class \:interval )/( 2)}}`

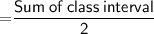
That is,

`\sf{=}{\sf{( = 18 + 25)/(2)}}`

`\sf{=}{\sf{( = 43)/(2)}}`

`\sf{= 21.5 }`

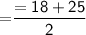
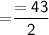
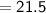
[ For more calculation ,Please refer the attachment ]

• For calculating fx
• Multiply frequency and midpoint

`\sf{ fx = frequency {*} midpoint }`

`\sf{ fx = 8 {*} 21.5 }`

`\sf{ fx = 172 }`

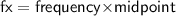
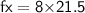
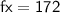
[ For more calculation please refer the attachment ]

Now,

We have to calculate mean, median and mode of the given data

For mean

We know that the,

Mean = Sum of all observation / no. of observation

That is

`\sf{ Mean = }{\sf{\frac{ {\sigma}fx}{{\sigma}x}}}`

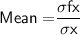
Subsitute the required values,

`\sf{ Mean = }{\sf{( 1811 )/( 187.5)}}`

`\sf{ Mean = 9.65}`

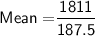
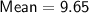
Hence, The mean of the given data is 9.65

For Median

We know that, For odd numbers

`\sf{ Median = l + }{\sf{( (n/2 - c))/( f)}}{\sf{ h }}`

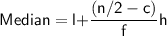
Here,

`\sf{ n = }{\sf{( 50 + 1)/( 2)}}`

`\sf{ n = }{\sf{( 50 )/( 2)}}`

`\sf{ n = 25 }`

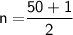
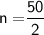
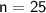
• Lower limit = 34
• c = 20
• f = 14
• h = 41 - 34 = 7

Subsitute the required values in the above formula :-

`\sf{ Median = 34 + }{\sf{( (25-20))/( 14)}}{\sf{ 7 }}`

`\sf{ = 34 + }{\sf{( 5)/( 14)}}{\sf{ {*}7 }}`

`\sf{ = 34 + }{\sf{( 35)/( 14)}}`

`\sf{ = 34 + 2.5}`

`\sf{ = 36.5 }`

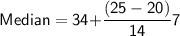
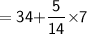
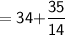
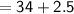
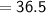
Hence, The median of the given data is 36.5 .

For Mode

We know that,

`\sf{ M= l }{\sf{( (f1 - fo))/( 2f1 - fo - f2 )}}{\sf{ {*} h }}`

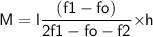
• lower limit = 34
• f1 = 14
• fo = 12
• f2 = 12
• H = 7

Subsitute the required values,

`\sf{ M= 34 }{\sf{( (14 - 12))/( 2(14)- 12 - 12 )}}{\sf{ {*} 7 }}`

`\sf{ M= 34{*}}{\sf{( 2)/( 28 - 24 )}}{\sf{ {*} 7 }}`

`\sf{ M= 34{*}}{\sf{( 2)/( 4 )}}{\sf{ {*} 7 }}`

`\sf{ M= 34{*}}{\sf{( 1)/( 2 )}}{\sf{ {*} 7 }}`

`\sf{ M= 34{*}}{\sf{( 7)/( 2 )}}`

`\sf{ M= 34 + 3.5 }`

`\sf{ M= 37.5 }`

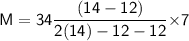
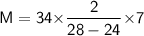
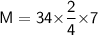
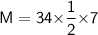
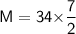
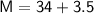
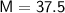
So,

• Mode = 37.5

Hence ,The mode of the given data is 37.5 .