What is the inverse of:f(x)=x^3+5

Question

What is the inverse of:
`f(x)=x^3+5`

Answer 1

f⁻¹(x) = ∛x-5

Explanation:

y = x³ + 5

x = y³ + 5 ... replace x with y

y³ = x-5

y = ∛x-5

Answer 2

`\displaystyle \large{ {f}^( - 1) (x) = \sqrt[3]{x - 5} }`

Explanation:

To find an inverse, we swap x to f(x)/y and f(x)/y to x.

We are given:-

`\displaystyle \large{f(x) = {x}^(3) + 5}`

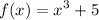
Swap:-

To make the equation look better and easier to simplify, we will be changing f(x) to y.

Thus:-

`\displaystyle \large{y= {x}^(3) + 5} \\ \displaystyle \large{x= {y}^(3) + 5}`

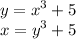
Now simplify to y-isolated.

Subtract both sides by 5.

`\displaystyle \large{x - 5= {y}^(3) + 5 - 5} \\ \displaystyle \large{x - 5= {y}^(3) }`

Cube root both sides.

`\displaystyle \large{ \sqrt[3]{x - 5} = \sqrt[3]{ {y}^(3) } } \\ \displaystyle \large{ \sqrt[3]{x - 5} = y }`

Convert y to f(x) and add exponent of -1 between f and (x).

`\displaystyle \large{ \sqrt[3]{x - 5} = {f}^( - 1) (x) }`

To indicate that the function is an inverse.

And we're done!