Answer:
![\displaystyle \large{ {f}^( - 1) (x) = \sqrt[3]{x - 5} }](https://img.qammunity.org/2022/formulas/mathematics/high-school/7j4lhc8h4z8yvb6cki8hs7vlayyul6togo.png)
Explanation:
To find an inverse, we swap x to f(x)/y and f(x)/y to x.
We are given:-
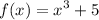
Swap:-
To make the equation look better and easier to simplify, we will be changing f(x) to y.
Thus:-
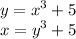
Now simplify to y-isolated.
Subtract both sides by 5.
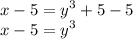
Cube root both sides.
![\displaystyle \large{ \sqrt[3]{x - 5} = \sqrt[3]{ {y}^(3) } } \\ \displaystyle \large{ \sqrt[3]{x - 5} = y }](https://img.qammunity.org/2022/formulas/mathematics/high-school/k4gidvp7pi07trbed54gy3trll0tn8vkiv.png)
Convert y to f(x) and add exponent of -1 between f and (x).
![\displaystyle \large{ \sqrt[3]{x - 5} = {f}^( - 1) (x) }](https://img.qammunity.org/2022/formulas/mathematics/high-school/x27xvnwkoxvxge1f82axdh0azy0v4e6a8l.png)
To indicate that the function is an inverse.
And we're done!