Question

`8 * √(2) = {2}^(n)`
work out the Value of n
with steps ​

Answer 1

n = 7/2

Explanation:

We are given the equation:-

`\displaystyle \large{8 * √(2) = {2}^(n) }`

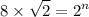
To solve an exponential equation, first, we convert the whole equation with same base.

Let our main base is 2 for whole equation, the following number must be:-

• 8 = 2•2•2 = 2^3
• √2 = 2^(1/2) —> Law of Exponent

From √2 = 2^(1/2) comes from:-

`\displaystyle \large{ {a}^{ (m)/( n ) } = \sqrt[n]{ {a}^(m) } }`

• m = 1
• n = 2
• a = 2

`\displaystyle \large{ {2}^{ (1)/( 2 ) } = √(2) }`

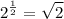
Rewrite the equation with base 2.

`\displaystyle \large{ {2}^(3) * {2}^{ (1)/(2) } = {2}^(n) }`

Recall the law of exponent:-

`\displaystyle \large{ {a}^(m) * {a}^(n) = {a}^(m + n) }`

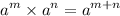
Therefore:-

`\displaystyle \large{ {2}^{3 + (1)/(2) } = {2}^(n) } \\ \displaystyle \large{ {2}^{ (6)/(2) + (1)/(2) } = {2}^(n) } \\ \displaystyle \large{ {2}^{ (7)/(2) } = {2}^(n) }`

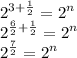
Compare the exponent and thus:-

n = 7/2.