Answer:
n = 7/2
Explanation:
We are given the equation:-
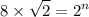
To solve an exponential equation, first, we convert the whole equation with same base.
Let our main base is 2 for whole equation, the following number must be:-
- 8 = 2•2•2 = 2^3
- √2 = 2^(1/2) —> Law of Exponent
From √2 = 2^(1/2) comes from:-
![\displaystyle \large{ {a}^{ (m)/( n ) } = \sqrt[n]{ {a}^(m) } }](https://img.qammunity.org/2022/formulas/mathematics/high-school/z2mweo5ebtii10ge1ejgfhagehkmekcs2z.png)
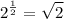
Rewrite the equation with base 2.
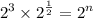
Recall the law of exponent:-
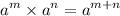
Therefore:-
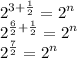
Compare the exponent and thus:-
n = 7/2.