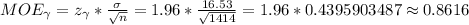Question

The General Social Survey included a question about how many hours the respondent spent doing volunteer activities outside of their own home. For the 1,414 respondents, the sample mean was 6.15 hours and the sample standard deviation was 16.53 hours. Find the margin of error for a 95% confidence interval for the population mean amount of time spent doing volunteer activities outside of their own home.

2.320


0.864


6.15


2.135

Answer 1

Closest answer is B

Explanation:

Recall:

• Margin of error:
  `MOE_\gamma=z_\gamma*{(\sigma)/(√(n))}`

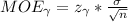
• Critical value:
  `z_\gamma`
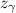
• Standard deviation:
  `\sigma`
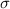
• Sample size:
  `n`

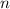
Given:

• Standard deviation:
  `\sigma=16.53`
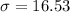
• Sample size:
  `n=1414`
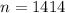
• Confidence level:
  `C=0.95`

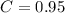
Determine critical value given confidence interval:

• 
  `z_\gamma=1.96`

Determine margin of error:

• Margin of error:
  `MOE_\gamma=z_\gamma*{(\sigma)/(√(n))}=1.96*{(16.53)/(√(1414))}=1.96*0.4395903487\approx0.8616`