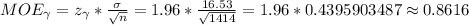Answer:
Closest answer is B
Explanation:
Recall:
- Margin of error:
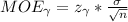
- Critical value:
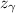
- Standard deviation:

- Sample size:

Given:
- Standard deviation:
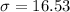
- Sample size:

- Confidence level:

Determine critical value given confidence interval:
Determine margin of error:
- Margin of error: