Answer:
Approximately
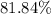 .
.
Step-by-step explanation:
Balanced equation for this reaction:
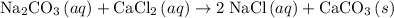 .
.
Look up the relative atomic mass of elements in the limiting reactant,
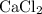 , as well as those in the product of interest,
, as well as those in the product of interest,
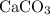 :
:
Calculate the formula mass for both the limiting reactant and the product of interest:
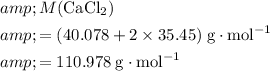 .
.
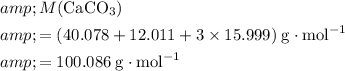 .
.
Calculate the quantity of the limiting reactant (
 ) available to this reaction:
) available to this reaction:
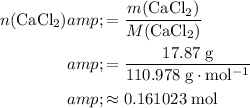 .
.
Refer to the balanced equation for this reaction. The coefficients of the limiting reactant (
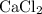 ) and the product (
) and the product (
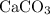 ) are both
) are both
 . Thus:
. Thus:
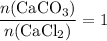 .
.
In other words, for every
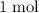 of
of
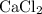 formula units that are consumed,
formula units that are consumed,
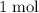 of
of
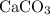 formula units would (in theory) be produced. Thus, calculate the theoretical yield of
formula units would (in theory) be produced. Thus, calculate the theoretical yield of
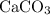 in this experiment:
in this experiment:
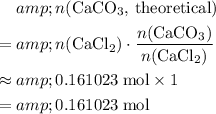 .
.
Calculate the theoretical yield of this experiment in terms of the mass of
 expected to be produced:
expected to be produced:
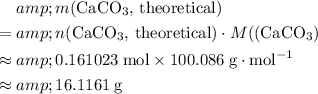 .
.
Given that the actual yield in this question (in terms of the mass of
 ) is
) is
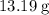 , calculate the percentage yield of this experiment:
, calculate the percentage yield of this experiment:
 .
.