(a) Fill in the table using the given rules for scoring. For example, if the coin shows heads and the die shows 1, then the score is 2 × 1 = 2; if the coin shows tails and die shows 1, then the score is 1 + 1 = 2.
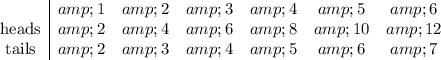
(b) A score of 4 can happen if the outcome is either
• heads and 2, or
• tails and 3
These events are mutually exclusive, meaning
Pr[(heads and 2) or (tails and 3)] = Pr[heads and 2] + Pr[tails and 3]
The coin toss and die roll are independent, so
Pr[heads and 2] = Pr[heads] × Pr[2] = 1/2 × 1/6 = 1/12
Pr[tails and 3] = Pr[tails] × Pr[3] = 1/2 × 1/6 = 1/12
Then
Pr[(heads and 2) or (tails and 3)] = 1/12 + 1/12 = 1/6
Put another way, there are 12 possible outcomes of the coin toss and die roll, and each has the same probability of occurring, 1/12. (This is because the results of the coin toss have equal probability, 1/2, and so do the results of the die roll, 1/6; by independence, each outcome can occur with probability 1/2 × 1/6 = 1/12.)
(c) Scoring 10 points has a probability of 1/12. Out of 60 games, George can expect to win 10 points 60 × 1/12 = 5 times.