Consider the expression
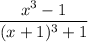
Factorize the numerator and denominator a difference/sum of cubes:
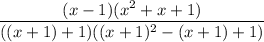
Expand the denominator:
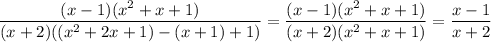
since x = 2020, and clearly 2020² + 2020 + 1 ≠ 0, so we can cancel the factor of x ² + x + 1. This leaves us with
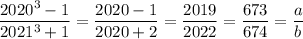
so that a + b = 673 + 674 = 1347.