Question

The fraction a/b is in simplest terms and equal to the following:((2020^3)-1)/((2021^3)+1) . What is a + b?

Answer 1

Consider the expression

`(x^3-1)/((x+1)^3+1)`

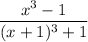
Factorize the numerator and denominator a difference/sum of cubes:

`((x-1)(x^2+x+1))/(((x+1)+1)((x+1)^2-(x+1)+1))`

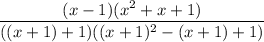
Expand the denominator:

`((x-1)(x^2+x+1))/((x+2)((x^2+2x+1)-(x+1)+1))=((x-1)(x^2+x+1))/((x+2)(x^2+x+1))=(x-1)/(x+2)`

since x = 2020, and clearly 2020² + 2020 + 1 ≠ 0, so we can cancel the factor of x ² + x + 1. This leaves us with

`(2020^3-1)/(2021^3+1) = (2020-1)/(2020+2) = (2019)/(2022)=(673)/(674)=\frac ab`

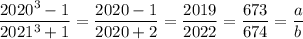
so that a + b = 673 + 674 = 1347.