f ' (0) exists if the limit,
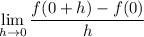
exists, and f ' (0) has the value of this limit.
In order for this limit to exist, both limits from either side of h = 0 must exist.
Suppose h < 0. Then 0 + h is also negative, so by definition of f(x) we have
f (0 + h) = ((0 + h) + 1)² = h ² + 2h + 1
Then in the limit, if h is approaching 0, it must be from below or from the left:
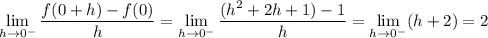
Now suppose h > 0, so that 0 + h is positive and h approaches 0 from above or from the right. Then
f (0 + h) = 2 (0 + h) + 1 = 2h + 1
and
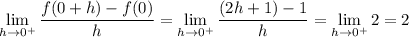
Both one-sided limits match, so f ' (0) = 2.