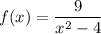(i) The graph of f is symmetric about the y-axis - this is another way of saying f is an even function, which means
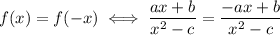
The denominator remains unchanged, so
ax + b = -ax + b
Solve for a :
ax = -ax
2ax = 0
a = 0
(The alternative is that x = 0, but if that were the case then there would be infinitely many choices for a.)
So
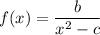
(ii) Since
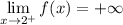
it follows that x - 2 must be a factor of the denominator. If that's true, then
x ² - c = (x - 2) (x - r )
for some other root r of x ² - c. Expanding the right side gives
x ² - c = x ² - (2 + r )x + 2r
so that
-(2 + r ) = 0 ===> r = -2
2r = -c ===> -c = -4 ===> c = 4
and so
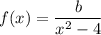
(iii) Finally, we're given that f ' (1) = -2. Differentiating f gives
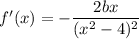
so that
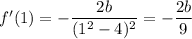
Then
-2b/9 = -2 ===> b = 9
and we find that