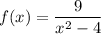Question

How to determine values of a,b and c

Answer 1

(i) The graph of f is symmetric about the y-axis - this is another way of saying f is an even function, which means

`f(x) = f(-x) \iff (ax+b)/(x^2-c) = (-ax+b)/(x^2-c)`

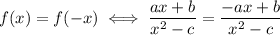
The denominator remains unchanged, so

ax + b = -ax + b

Solve for a :

ax = -ax

2ax = 0

a = 0

(The alternative is that x = 0, but if that were the case then there would be infinitely many choices for a.)

So

`f(x) = (b)/(x^2-c)`

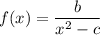
(ii) Since

`\displaystyle \lim_(x\to2^+)f(x) = +\infty`

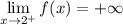
it follows that x - 2 must be a factor of the denominator. If that's true, then

x ² - c = (x - 2) (x - r )

for some other root r of x ² - c. Expanding the right side gives

x ² - c = x ² - (2 + r )x + 2r

so that

-(2 + r ) = 0 ===> r = -2

2r = -c ===> -c = -4 ===> c = 4

and so

`f(x) = (b)/(x^2-4)`

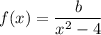
(iii) Finally, we're given that f ' (1) = -2. Differentiating f gives

`f'(x) = -(2bx)/((x^2-4)^2)`

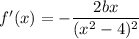
so that

`f'(1) = -(2b)/((1^2-4)^2) = -(2b)/(9)`

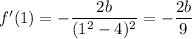
Then

-2b/9 = -2 ===> b = 9

and we find that

`f(x) = (9)/(x^2-4)`