Answer:
x = -
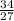 and y =
and y =
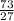
Explanation:
2x + 5y = 11
7x + 4y = 2
Let's try elimination here since we have a system of equations:
-7(2x + 5y = 11) = -14x - 35y = -77
and
2(7x + 4y = 2) = 14x + 8y = 4
The x's cancel out now so let's combine the two equations:
-35 + 8 = -27
-77 + 4 = -73
-27y = -73
y =
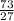
Now that we have y's value, let's plug that value in for y in the other equation. You may choose whichever equation you want to solve for x but it is recommended to use the easiest one. (Since this value is complicated, it won't really matter.)
2x + 5(
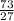 ) = 11
) = 11
2x +
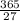 = 11
= 11
2x = -
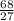
x = -
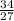
To check and make sure you have the correct values, plug both values into the orginal equation and make sure the equation is true.