First of all, recall the definition of absolute value:
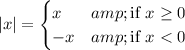
So if x < 4, then x - 4 < 0, so |x - 4| = -(x - 4), and the first case in h(x) reduces to
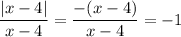
Next, in order for h(x) to be continuous at x = 4, the limits from either side of x = 4 must be equal and have the same value as h(x) at x = 4. From the given definition of h(x), we have
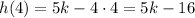
Compute the one-sided limits:
• From the left:
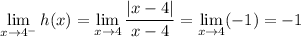
• From the right:
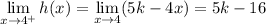
If the limits are to be equal, then
-1 = 5k - 16
Solve for k :
-1 = 5k - 16
15 = 5k
k = 3