Question

HELPPPPPP

h(x)=-(x-2)^2+7

A) Restrict the domain of h(x) to make it invertible

B)Find h^(-1)(x), in terms of x.

C) What is the range and domain of h^(-1)(x)

Answer 1

If
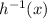`h^(-1)(x)` is the inverse of
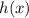`h(x)`, then

`h\left(h^(-1)(x)\right) = x`

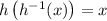
Given that
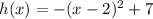`h(x)=-(x-2)^2+7`, we have

`h\left(h^(-1)(x)\right) = -\left(h^(-1)(x)-2\right)^2 + 7 = x`

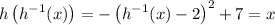
Solve for the inverse :

`-\left(h^(-1)(x)-2\right)^2 + 7 = x \\\\ -\left(h^(-1)(x)-2\right)^2 = x-7 \\\\ \left(h^(-1)(x)-2\right)^2 = 7-x \\\\ \sqrt{\left(h^(-1)(x)-2\right)^2} = √(7-x) \\\\ \left|h^(-1)(x)-2\right| = √(7-x)`

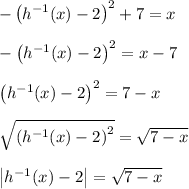
At this point, we have two possible solutions:

• If
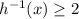`h^(-1)(x)\ge2`, then
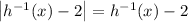`\left|h^(-1)(x)-2\right| = h^(-1)(x)-2`. Continuing with the equation, we have

`h^(-1)(x) - 2 = √(7-x) \\\\ h^(-1)(x) = 2 + √(7-x)`

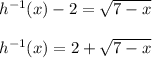
• Otherwise, if
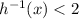`h^(-1)(x)<2`, then
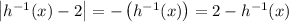`\left|h^(-1)(x)-2\right|=-\left(h^(-1)(x)\right)=2-h^(-1)(x)`, in which case

`2-h^(-1)(x) = √(7-x) \\\\ h^(-1)(x) = 2 - √(7-x)`

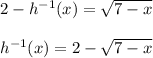
Both solutions are simultaneously incompatible. For instance, when x = 0 we have
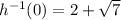`h^(-1)(0)=2+\sqrt7` using the first solution, and
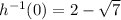`h^(-1)(0)=2-\sqrt7` using the second one. Choosing one over the other depends on how you restrict the domain.

(A) If we want to stick with the first solution, we would required that x ≥ 2. In other words, we would have
`h(x)` defined only when x ≥ 2; then
`h\left(h^(-1)(x)\right)` is defined only when
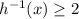`h^(-1)(x)\ge2`, so that ...

(B) ... the inverse is

`\boxed{h^(-1)(x)=2+√(7-x)}`

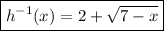
(C) The domain of the inverse is the same as the range of the original function, and vice versa.

• Domain: we have for all x that

`-(x-2)^2 \le 0`

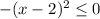
so

`-(x-2)^2 + 7 \le 7`

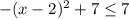
which means the range of
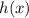`h(x)`, and hence the domain of
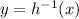`y=h^(-1)(x)`, is

`\left\{y \mid y \le 7\}`

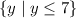
• Range: we get this immediately from the domain restriction we chose earlier,

`\left\{x \mid x \ge 2\}`

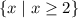
See the attached plot -
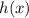`h(x)` is shown as a dashed orange curve;
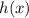`h(x)` with the restricted domain is shown in blue; the inverse
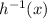`h^(-1)(x)` corresponding to the restricted
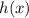`h(x)` is shown in green; the other inverse is shown with a dashed red curve. You can see a geometrical properties of inverses: if you mirror the blue curve along the dotted line (y = x), you would get the green curve.