1 Answer

Geddon · Answer 1 · 2022-06-01T05:43:09+0000

Explanation:

$\large\underline{\sf{Solution-}}$

Given that lines makes an angle α, β, γ with x - axis, y - axis and z - axis respectively.

So, By definition of direction cosines,

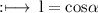
$\rm :\longmapsto\:l = cos \alpha$

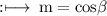
$\rm :\longmapsto\:m = cos \beta$

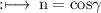
$\rm :\longmapsto\:n = cos \gamma$

So,

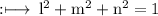
$\rm :\longmapsto\: {l}^(2) + {m}^(2) + {n}^(2) = 1$

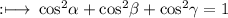
$\rm :\longmapsto\: {cos}^(2) \alpha + {cos}^(2) \beta + {cos}^(2) \gamma = 1$

On multiply by 2 on both sides we get

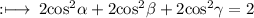
$\rm :\longmapsto\: 2{cos}^(2) \alpha + 2{cos}^(2) \beta + 2 {cos}^(2) \gamma = 2$

can be further rewritten as

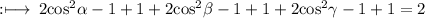
$\rm :\longmapsto\: 2{cos}^(2) \alpha - 1 + 1 + 2{cos}^(2) \beta - 1 + 1 + 2 {cos}^(2) \gamma - 1 + 1 = 2$

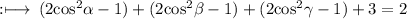
$\rm :\longmapsto\: (2{cos}^(2) \alpha - 1)+ (2{cos}^(2) \beta - 1)+ (2 {cos}^(2) \gamma - 1) + 3= 2$

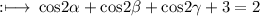
$\rm :\longmapsto\:cos2 \alpha + cos2 \beta + cos2 \gamma + 3= 2$

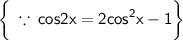
$\red{ \bigg\{ \sf \: \because \: cos2x = {2cos}^(2)x - 1 \bigg\}}$

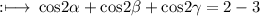
$\rm :\longmapsto\:cos2 \alpha + cos2 \beta + cos2 \gamma= 2 - 3$

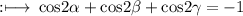
$\rm :\longmapsto\:cos2 \alpha + cos2 \beta + cos2 \gamma= - 1$

Hence,

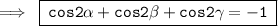
$\bf\implies \:\boxed{\tt{ \: cos2 \alpha + cos2 \beta + cos2 \gamma = - 1 \: }}$

So, option (d) is correct.

▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬

Direction cosines of a line segment is defined as the cosines of the angle which a line makes with the positive direction of respective axis.

The scalar components of unit vector always give direction cosines.

The scalar components of a vector gives direction ratios.

Please log in or register to add a comment.