Question

What can be the solution process for this​

Answer 1

x = 4/5

Explanation:

We are given the equation:

`\displaystyle \large{ (5x - 4)/( √(5x) + 2 ) = 2 - ( √(5x) + 2)/(2) }`

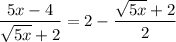
Multiply both sides by LCM which is 2(√5x +2) to clear out the denominator.

`\displaystyle \large{ (5x - 4)/( √(5x) + 2 )(2)(√(5x) + 2)= 2 (2)( √(5x) + 2) - ( √(5x) + 2)/(2) (2)( √(5x + 2) )} \\ \displaystyle \large{ (5x - 4)2= 4( √(5x) + 2) - (√(5x) + 2)( √(5x) + 2)} \\ \displaystyle \large{ 10x - 8= 4√(5x) + 8 - ( √(5x) + 2) ^(2) } \\ \displaystyle \large{ 10x - 8= 4√(5x) + 8 - (5x + 4 √(5x) + 4) } \\ \displaystyle \large{ 10x - 8= 4√(5x) + 8 - 5x - 4 √(5x) - 4} \\ \displaystyle \large{ 10x - 8= 4 - 5x}`

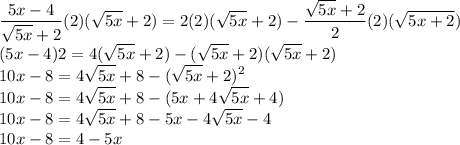
Thus, our simplified equation is;-

`\displaystyle \large{10x - 8 = 4 - 5x}`

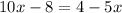
Add both sides by 5x then add both sides by 8.

`\displaystyle \large{10x + 5x - 8 = 4 - 5x + 5x} \\ \displaystyle \large{15x - 8 = 4} \\ \displaystyle \large{15x - 8 + 8 = 4 + 8} \\ \displaystyle \large{15x= 12}`

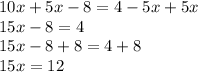
Divide both sides by 15.

`\displaystyle \large{ (15x)/(15) = (12)/(15) } \\ \displaystyle \large{x = (4)/(5) }`

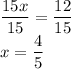
Therefore, x = 4/5