Question

Prove that: √(sec x + 1)/(sec x - 1) = 1/(cosec x - cot x) ​

Answer 1

Sorry Bro

Explanation:

I don't know the ans plzz donnot mind

Answer 2

`\large\underline{\sf{Solution-}}`

Consider LHS

`\rm :\longmapsto\: \sqrt{(secx + 1)/(secx - 1) }`

can be rewritten as

`\rm \:  =  \: \sqrt{((1)/(cosx) + 1 )/((1)/(cosx) - 1) }`

`\rm \:  =  \: \sqrt{((1 + cosx)/(cosx))/((1 - cosx)/(cosx)) }`

`\rm \:  =  \: \sqrt{(1 + cosx)/(1 - cosx) }`

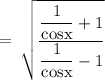
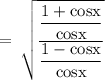
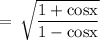
On rationalizing the numerator, we get

`\rm \:  =  \: \sqrt{(1 + cosx)/(1 - cosx) * (1 - cosx)/(1 - cosx) }`

`\rm \:  =  \: \sqrt{\frac{1 - {cos}^(2) x}{ {(1 - cosx)}^(2) } }`

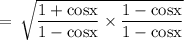
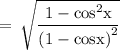
We know,

`\red{\rm :\longmapsto\:\boxed{\tt{ {sin}^(2)x + {cos}^(2)x = 1}}}`

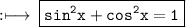
So, using this, we get

`\rm \:  =  \: \frac{ \sqrt{ {sin}^(2) x} }{1 - cosx}`

`\rm \:  =  \: ( sinx )/(1 - cosx)`

`\rm \:  =  \: (1)/( \: \: \: \: (1 - cosx)/(sinx) \: \: \: \: )`

`\rm \:  =  \: (1)/( \: \: \: \: (1)/(sinx) - (cosx)/(sinx) \: \: \: \: )`

`\rm \:  =  \: (1)/( \: \: \: \: cosecx - cotx \: \: \: \: )`

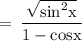
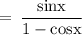
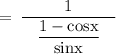
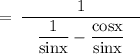
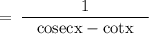
Hence, Proved

`\rm \implies\:\: \boxed{\tt{ \sqrt{(secx + 1)/(secx - 1) } = (1)/(cosecx - cotx)}}`

▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬

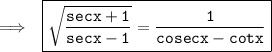
MORE TO KNOW

Additional Information:-

Relationship between sides and T ratios

sin θ = Opposite Side/Hypotenuse

cos θ = Adjacent Side/Hypotenuse

tan θ = Opposite Side/Adjacent Side

sec θ = Hypotenuse/Adjacent Side

cosec θ = Hypotenuse/Opposite Side

cot θ = Adjacent Side/Opposite Side

Reciprocal Identities

cosec θ = 1/sin θ

sec θ = 1/cos θ

cot θ = 1/tan θ

sin θ = 1/cosec θ

cos θ = 1/sec θ

tan θ = 1/cot θ

Co-function Identities

sin (90°−x) = cos x

cos (90°−x) = sin x

tan (90°−x) = cot x

cot (90°−x) = tan x

sec (90°−x) = cosec x

cosec (90°−x) = sec x

Fundamental Trigonometric Identities

sin²θ + cos²θ = 1

sec²θ - tan²θ = 1

cosec²θ - cot²θ = 1