Question

Answer plss asap i beg

Answer 1

Answer: number 2

Step-by-step explanation: Give me a thank please

Answer 2

3²

Explanation:

You can rewrite the given problem as follows:

`3^(-6) * ((3^(4) )/(3^(0) ))^(2)`

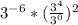
The first thing you must do is work on the terms inside the parenthesis.

According to the Zero exponent rule:
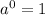`a^(0) = 1`. This means that any number or variable raised to the 0 power will equal 1. Therefore, the denominator inside the parenthesis is 1.

`3^(-6) * ((3^(4) )/(1))^(2)`

`= 3^(-6) * (3^(4))^(2)`

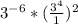
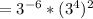
Next, according to the Power-to-Power Rule:
`(a^(m))^(n) = a^(m*n)`

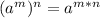
Therefore, you can multiply the exponent, 2, into
`3^(4)`:

`= 3^(-6) * 3^((4*2))`

`= 3^(-6) * 3^(8)`

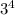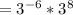
Then, the you can also apply the Negative Exponent Rule for rewriting
`3^(-6)`:

`a^(-n) = (1)/(a^(n) )`

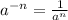
Therefore,
`3^(-6)` will become:
`3^(-6) = (1)/(3^(6) )`

`= (1)/(3^(6)) * 3^(8) = (3^(8))/(3^(6))`

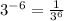
Finally, the Quotient Rule states that:

`(a^(m) )/(a^(n) ) = a^((m-n))`

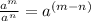
Therefore:

`(3^(8) )/(3^(6) ) = 3^((8-6)) = 3^(2)`

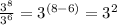
The correct answer is 3²