Answer:
y = 5/4x + 7
Explanation:
Given points (-4, 2) and (-8, -3):
Let (x1, y1) = (-4, 2)
(x2, y2) = (-8, -3)
Use these points to solve for the slope of the line:
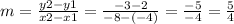
Therefore, the slope of the line is: m = 5/4.
Next, we must determine the y-intercept. In order to do so, we can use the point-slope form and plug in the values of (-4, 2) into the equation as (x1, y1):
y - y1 = m(x - x1)
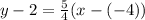

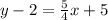
Add 2 on both sides of the equation:
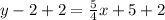
y = 5/4x + 7
Therefore, the equation of the line is: y = 5/4x + 7 where the slope (m) is 5/4, and the y-intercept (b) is 7.