Question

I need help please. Thanks in advance.

Answer 1

Angle KLN = 125 degrees

Angle NLM = 55 degrees

Explanation:

Angle KLM is a straight angle; it must be 180 degrees. We can write the equation (10x-5)+(4x+3)=180, based on this statement. Because the order of operation does not apply to addition and subtract, we can remove the paratheses and combine like-terms. 10x+4x-5+3=180 can be simplified to 14x-2=180. Upon solving this equation, we get x=13. We now must plug 13 in for x in both of the original angle measurements. When x=13 in (10x-5), we get 125. When x=13 in (4x+3), we get 55. :)

Answer 2

m < KLN = 125°

m < NLM = 55°

Explanation:

Given that < KLM is a straight angle:

Then it means that the sum of the measures of < KLN and < NLM = 180°.

Thus, we can setup the following equation to find their measures:

m < KLN + m < NLM = 180°

where m < KLN = (10x - 5)°

m < NLM = (4x + 3)°

Substitute these values into the formula:

m < KLN + m < NLM = 180°

10x - 5 + 4x + 3 = 180°

Combine like terms:

14x - 2 = 180°

Add 2 on both sides of the equation:

14x - 2 + 2 = 180° + 2

14x = 182

Divide both sides by 14 to solve for x:

`(14x)/(14) = (182)/(14)`

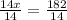
x = 13°

We can substitute x = 13° into the given values of each angle to determine their actual measures:

m < KLN = [10(13) - 5]° = 130 - 5 = 125°

m < NLM = [4(13) + 3]° = 52 + 3 = 55°

Double-check to see whether the measures of these two angles add up to 180°:

m < KLN + m < NLM = 180°

125° + 55° = 180°

180° = 180° (True statement). Therefore, our derived answers were correct.