Answer:
h = 1.81 cm
Explanation:
Using the equation for the volume of the cylinder:
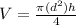
We need to isolate h by doing the follwing steps:
Eliminate the fraction by multiplying both sides by 4:
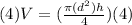
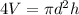
Next, divide both sides by πd² to isolate h:
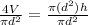
Therefore, the formula for h is:
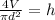
Next, plug in the values for d and V:
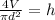
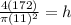
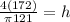
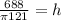
1.81 = h
Therefore, h = 1.81 cm