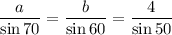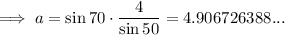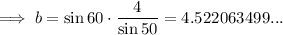Answer:
Sum of interior angles of a triangle = 180°
Sine rule to find side lengths:
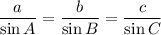
----------------------------------------------------------------------
Question 1a
Given: A = 40°, B = 20°, a = 2
40° + 20° + C = 180°
⇒ C = 120°
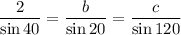
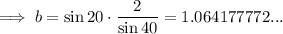
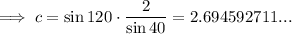
----------------------------------------------------------------------
Question 2b
Given: A = 50°, C = 20°, a = 3
50° + 20° + B = 180°
⇒ B = 110°
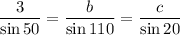
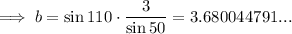
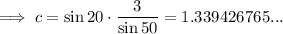
----------------------------------------------------------------------
Question 3c
Given: B = 70°, C = 10°, b = 5
70° + 10° + A = 180°
⇒ A = 100°
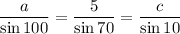
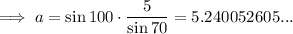
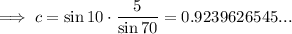
----------------------------------------------------------------------
Question 4d
Given: A = 70°, B = 60°, c = 4
70° + 60° + C = 180°
⇒ C = 50°