Answer:
Parallel:
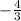
Perpendicular:
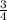
Explanation:
Hello!
First, we need to find the slope of the given line. Convert it into Slope-Intercept Form.
Slope - Intercept Form:

Convert
Parallel Lines
Parallel lines have the same slope but an altered y-intercept. Therefore, the slope of the line parallel to this one is also
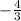 .
.
Perpendicular Lines
Perpendicular lines have an opposite reciprocal slope. That means you flip the sign (+/-) and flip the numerator and denominator. The slope of the line perpendicular to this one is
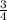 .
.