Answer:
36%
Explanation:
Area of circle is
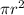
If the radius is decreased by 20%. Then the radius will be
80% of the original radius.
So our radius is 0.8.
So our area is
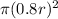
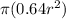
Since pi is constant, the radius only really matters.
We went from
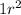
to
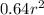
So our area will decrease by 36%
Proof: Let the radius be 10.
So the area of circle will be
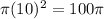
Let our other radius is 8 because 8 is a 20% decrease of the orginal radius
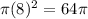
Next, we subtract the area to find decrease in area

Since pi is constant, we can ignore it so our decrease in area is 36%