We are given the Indefinite integral ;
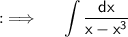
Take x common from denominator ;
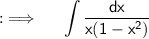
Now , Put ;
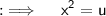
So that ;
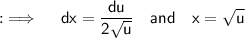
Now , putting the values ;
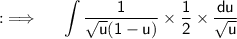
Now , as constant can be taken out of the integrand, so now ;
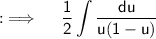
Using partial fraction decomposition, Rewrite the integral as ;
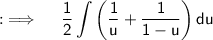
As Integrals follow distributive property, so breaking the integral into two integrals, and continuing the integration
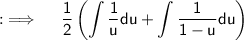
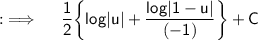
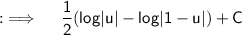
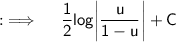
Putting value of u ;
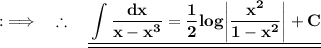
This is the required answer
Used Concepts :-