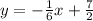Answer:
Explanation:
The slope of the line perpendicular is always the negative reciprocal of the line you're given.
So, in this case, the slope in y = 6x + 4, is 6 (the coefficient in front of the x). The negative of this is -6, and then do the reciprocal which is -1/6.
Next, we are given the the point that it passes through, which is (-3, 4). We have to use point slope formula for this which is given by:
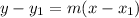
We know m = -1/6 from before, and
 , and
, and
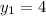 (this comes from the given point). Plugging these in we have:
(this comes from the given point). Plugging these in we have:
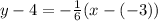
Point slope intercept form is given by
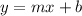 so to rearrange it to this form, we have to distribute the -1/6 and isolate y.
so to rearrange it to this form, we have to distribute the -1/6 and isolate y.
After distributing we get:
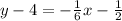
Then isolating the y term we get: