Question

For a set of scores, it was found that the mean score was 79 and the standard deviation was 17. If the distribution of scores is approximately normal, find the percentage of scores between: 45 and 113

(please show your work cause im hecka confused)

Answer 1

95%

Explanation:

In this question, it's important to note that the question states the distribution is a normal distribution, therefore we can use the Empirical Rule (68-95-99.7 rule).

The Empirical Rule, also known as the 68-95-99.7 rule, states that:

• 68% of data falls between ±1 standard deviation from the mean

• 95% of data falls between ±2 standard deviations from the mean
• 99.7% of data falls between ±3 standard deviations from the mean

*Note that the Empirical Rule only works for normal distributions

We know that the mean,
`\mu`, is given as 79 and the standard deviation,
`\sigma`, is given as 17. Since the standard deviation is 17, 2 standard deviations must be
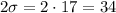`2\sigma=2\cdot 17=34` (and 3 standard deviations would just be 51).

We want to find the percentage of scores (% of data) that falls between the scores 45 and 113.

Notice that 45 is 34 less than the mean of 79 and 113 is 34 more than the mean of 79, therefore, the range of scores between 45 and 113 varies between ±2 standard deviations from the mean.

From the Empirical Rule, we can see that 95% of data falls between ±2 standard deviations in a normal distributions.

Thus, 95% of scores fall between 45 and 113.