Question

Can someone help to know how to do horizontal asymptote please?!??

Answer 1

See Explanation

Explanation:

In a rational equation, horizontal asymptotes are based on the highest degree of the polynomials on the numerator and denominator.

If it is top-heavy (higher degree on the numerator), then there is no asymptote.

Ex:
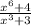`(x^(6) +4)/(x^(3) +3)`. The degree of the numerator is 6 and the denominator degree is 3; 6>3, so no asymptote.

If it is bottom-heavy (higher degree on denominator), then the x-axis (y=0) is the horizontal asymptote.

Ex:
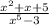`(x^(2)+x+5 )/(x^(5)-3)`. The highest degree of the numerator is 2 vs the highest degree of 5 on the denominator. Thus, the equation is bottom-heavy and the asymptote is at 0.

If the degrees are the same, you take the coefficient of the variables with the highest degrees and then divide.

Ex.
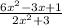`(6x^(2)-3x+1)/(2x^(2)+3)`. Take the coefficients of the x^2 (which is the highest degree variable). You should get 6 and 2. And then divide them in order to get:

y=6/2 = 3

Answer 2

The horizontal asymptote of a rational function can be determined by looking at the degrees of the numerator and denominator.

Degree of numerator is less than degree of denominator: horizontal asymptote at y = 0.

Degree of numerator is greater than degree of denominator by one: no horizontal asymptote; slant asymptote.