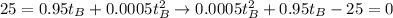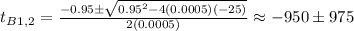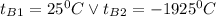Answer:
Step-by-step explanation:
From the case of well-stirred oil bath:
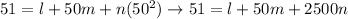
At the ice point, both of the thermometers show the same scale:
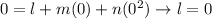
At the steam point, again, both of the thermometers show the same scale:
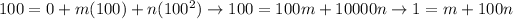
By eliminating those equations, we find:
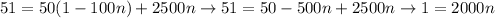
so we can obtain that:
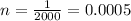 and
and
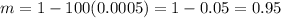
Now, we have the complete description of the relation between A and B scale as:
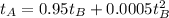
So, for
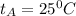 :
: