Answer:
About 27 years.
Explanation:
Byron deposits $13,500 in an account that earns 2.6% interest compounded monthly, and we want to determine how many years it will take for Byron's money to double.
Recall that compound interest is given by the formula:
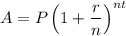
Since our initial deposit is $13,500 at a rate of 2.6% compounded monthly, P = 13500, r = 0.026, and n = 12:
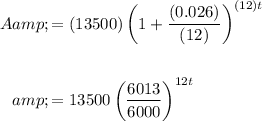
For his deposit to double, A must equal $27,000. Hence:
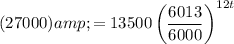
Solve for t:

In conclusion, it will take Byron about 27 years for his deposit to double.